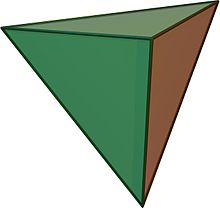
5 cellules - 5-cell

Régulier à 5 cellules (pentachore) (4-simplex)
Diagramme de Schlegel (sommets et arêtes)
Taper	Convexe régulier 4-polytope
Symbole Schläfli	{3,3,3}
Diagramme de Coxeter
Cellules	5 {3,3}
Visages	10 {3}
Bords	dix
Sommets	5
Figure de sommet	( tétraèdre )
Polygone de Pétrie	Pentagone
Groupe Coxeter	A 4 , [3,3,3]
Double	Auto-dual
Propriétés	convexe , isogonal , isotoxal , isoedrique
Indice uniforme	1

Figure de sommet : tétraèdre

Rapporter

En géométrie , le 5-cellule est le 4-polytope convexe régulier (analogue à quatre dimensions d'un solide platonicien) avec le symbole de Schläfli {3,3,3}. C'est un objet quadridimensionnel délimité par 5 cellules tétraédriques . Il est également connu sous le nom de pyramide C ₅ , pentachore , pentatope , pentaèdre ou tétraédrique . C'est le 4- simple ( polytope de Coxeter ), le 4-polytope régulier convexe le plus simple possible (analogue à quatre dimensions d'un solide platonicien ), et est analogue au tétraèdre à trois dimensions et au triangle à deux dimensions. Le pentachore est une pyramide à quatre dimensions à base tétraédrique. ${\displaystyle \alpha _{4}}$

La 5-cellule régulière est délimitée par 5 tétraèdres réguliers , et est l'un des six 4-polytopes convexes réguliers , représentés par le symbole de Schläfli {3,3,3}.

La cellule à 5 est une solution au problème : faites 10 triangles équilatéraux, tous de la même taille, en utilisant 10 allumettes, où chaque côté de chaque triangle est exactement une allumette. Aucune solution n'existe en trois dimensions.

L'enveloppe convexe de la 5-cellule et de son dual (en supposant qu'elles soient congruentes) est la disphénoïdale 30-cell , dual du bitruncate 5-cell .

Noms alternatifs

• Pentachoron
• 4-simplex
• Pentatope
• Pentaèdre (Henry Parker Manning)
• Stylo (Jonathan Bowers : pour pentachore)
• Hyperpyramide , pyramide tétraédrique

Géométrie

La cellule à 5 est auto-duale et sa figure de sommet est un tétraèdre. Son intersection maximale avec l'espace tridimensionnel est le prisme triangulaire . Son angle dièdre est cos ^-1 (1/4), soit environ 75,52°.

En tant que configuration

Cette matrice de configuration représente les 5 cellules. Les lignes et les colonnes correspondent aux sommets, aux arêtes, aux faces et aux cellules. Les nombres diagonaux indiquent combien de chaque élément se produit dans l'ensemble des 5 cellules. Les nombres non diagonaux indiquent combien d'éléments de la colonne se trouvent dans ou au niveau de l'élément de la ligne. La matrice de ce polytope auto-dual est identique à sa rotation de 180 degrés.

${\displaystyle {\begin{bmatrix}{\begin{matrix}5&4&6&4\\2&10&3&3\\3&3&10&2\\4&6&4&5\end{matrix}}\end{bmatrix}}}$

Construction

La 5-cellule peut être construite à partir d'un tétraèdre en ajoutant un 5ème sommet tel qu'il soit équidistant de tous les autres sommets du tétraèdre. (La cellule à 5 est une pyramide à 4 dimensions avec une base tétraédrique et quatre côtés tétraédriques.)

L'ensemble de coordonnées le plus simple est : (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (φ, φ, φ, φ), avec une longueur d'arête 2 √ 2 , où φ est le nombre d' or .

Les coordonnées cartésiennes des sommets d'une 5-cellule régulière centrée sur l'origine ayant une longueur d'arête 2 et un rayon √ 1,6 sont :

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3} }},\ \pm 1\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3 }}},\ 0\droit)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ ​​0\right)}$

${\displaystyle \left(-2{\sqrt {\frac {2}{5}}},\ 0,\ ​​0,\ ​​0\right)}$

Un autre ensemble de coordonnées centré sur l' origine en 4-espace peut être considéré comme un hyperpyramid avec une base tétraédrique régulière en 3-espace, avec une longueur d'arête 2 √ 2 et de rayon √ 3,2 :

${\displaystyle \left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(0,0,0,{\frac {4}{\sqrt {5}}}\right)}$

Les sommets d'un 4-simplex (avec arête √ 2 et rayon 1) peuvent être plus simplement construits sur un hyperplan en 5-espace, comme des permutations (distinctes) de (0,0,0,0,1) ou (0, 1,1,1,1) ; dans ces positions, c'est une facette respectivement du 5-orthoplexe ou du penteract rectifié .

Hélice de Boerdijk-Coxeter

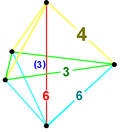
Une cellule à 5 peut être construite comme une hélice de Boerdijk-Coxeter de cinq tétraèdres enchaînés, pliés en un anneau à 4 dimensions. Les 10 faces triangulaires peuvent être vues dans un filet 2D dans un pavage triangulaire , avec 6 triangles autour de chaque sommet, bien que le pliage en 4 dimensions fasse coïncider les bords. Les bords violets représentent le polygone de Petrie de la 5-cellule.

Projections

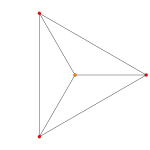
L' avion A ₄ Coxeter projette les 5 cellules dans un pentagone et un pentagramme réguliers . La projection plane A ₃ Coxeter des 5 cellules est celle d'une pyramide carrée . La projection plane A _{2 de} Coxeter de la cellule régulière à 5 est celle d'une bipyramide triangulaire (deux tétraèdres joints face à face) avec les deux sommets opposés centrés.

projections orthographiques

Un avion Coxeter k	Un 4	Un 3	Un 2
Graphique
Symétrie dièdre	[5]	[4]	[3]

Projections en 3 dimensions
Filaire de projection stéréographique (bord projeté sur une 3-sphère )	Une projection 3D d'une cellule à 5 effectuant une simple rotation
La projection vertex-first de la 5-cellule en 3 dimensions a une enveloppe de projection tétraédrique . Le sommet le plus proche des 5 cellules se projette vers le centre du tétraèdre, comme indiqué ici en rouge. La cellule la plus éloignée se projette sur l'enveloppe tétraédrique elle-même, tandis que les 4 autres cellules se projettent sur les 4 régions tétraédriques aplaties entourant le sommet central.	La projection de bord en premier de la cellule à 5 en 3 dimensions a une enveloppe dipyramidale triangulaire . Le bord le plus proche (montré ici en rouge) se projette sur l'axe de la dipyramide, les trois cellules qui l'entourent se projetant sur 3 volumes tétraédriques disposés autour de cet axe à 120 degrés les uns des autres. Les 2 cellules restantes se projettent sur les deux moitiés de la dipyramide et se trouvent de l'autre côté du pentatope.
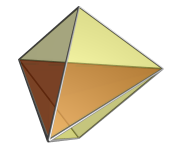La projection face première de la cellule à 5 en 3 dimensions a également une enveloppe dipyramidale triangulaire. Le visage le plus proche est représenté ici en rouge. Les deux alvéoles qui se rejoignent sur cette face se projettent sur les deux moitiés de la dipyramide. Les trois cellules restantes se trouvent de l'autre côté du pentatope du point de vue 4D et sont extraites de l'image pour plus de clarté. Ils sont disposés autour de l'axe central de la dipyramide, tout comme dans la projection du bord en premier.	La projection de la première cellule de la cellule à 5 en 3 dimensions a une enveloppe tétraédrique. La cellule la plus proche se projette sur toute l'enveloppe, et, du point de vue 4D, occulte les 4 autres cellules ; par conséquent, ils ne sont pas rendus ici.

5 cellules irrégulières

Il existe de nombreuses formes de symétrie inférieure, y compris celles que l'on trouve dans les figures de sommets polytopiques uniformes :

Symétrie	[3,3,3] Ordre 120	[3,3,1] Ordre 24	[3,2,1] Ordre 12	[3,1,1] Ordre 6	[5,2] + Ordre 10
Nom	5 cellules régulières	Pyramide tétraédrique	Pyramide triangulaire-pyramidale		Hyperdisphénoïde pentagonal
Schläfli	{3,3,3}	{3,3} ∨ ( )	{3} ∨ { }	{3} ( ) ( )
Exemple de figure de sommet	5-simplex	5-simplex tronqué	Bittronqué 5-simplex	5-simplex cantitronqué	Nid d'abeille 4-simplex omnitronqué

La pyramide tétraédrique est un cas particulier d'une 5 cellule , une pyramide polyédrique , réalisé sous forme régulière tétraèdre base dans un espace 3- hyperplan , et un sommet pointe au-dessus de l'hyperplan. Les quatre côtés de la pyramide sont constitués de cellules tétraédriques.

De nombreux 5-polytopes uniformes ont des figures de sommet de pyramide tétraédriques :

Symétrie [3,3,1], ordre 24

Diagramme de Schlegel
Nom Coxeter	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	t{3,3,3,3}	t{4,3,3,3}	t{3,4,3,3}

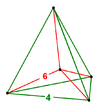
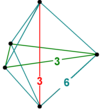
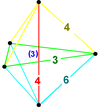
D'autres 5 polytopes uniformes ont des figures de sommet irrégulières à 5 cellules. La symétrie d'une figure de sommet d'un polytope uniforme est représentée en supprimant les nœuds annelés du diagramme de Coxeter.

Symétrie	[3,2,1], ordre 12		[3,1,1], ordre 6		[2 + ,4,1], ordre 8	[2,1,1], ordre 4
Diagramme de Schlegel
Nom Coxeter	t 12 α 5	t 12 γ 5	t 012 α 5	t 012 γ 5	t 123 α 5	t 123 γ 5

Symétrie	[2,1,1], ordre 2			[2 + ,1,1], ordre 2	[ ] + , commande 1
Diagramme de Schlegel
Nom Coxeter	t 0123 α 5	t 0123 γ 5	t 0123 β 5	t 01234 α 5	t 01234 γ 5

Composé

Le composé de deux 5 cellules dans des configurations doubles peut être vu dans cette projection plane de Coxeter A5 , avec des sommets et des bords à 5 cellules rouges et bleus. Ce composé a une symétrie [[3,3,3]], d'ordre 240. L'intersection de ces deux 5-cellules est une 5-cellule bitroncée uniforme . = ?? .

Ce composé peut être considéré comme l'analogue 4D de la 2D hexagramme { 6 / 2 } et la 3D composé de deux tétraèdres .

Polytopes et nids d'abeilles associés

Le 5-cellule est le premier dans la séquence de 6 4-polytopes réguliers convexes (par ordre de taille et de complexité).

4-polytopes convexes réguliers
Groupe Symétrie	Un 4	B 4		F 4	H 4
Nom	5 cellules hyper- tétraèdre	16 cellules Hyper- octaèdre	8 cellules Hyper- cube	24 cellules	600 cellules Hyper- icosaèdre	120 cellules Hyper- dodécaèdre
Symbole Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Diagramme de Coxeter
Graphique
Sommets	5	8	16	24	120	600
Bords	dix	24	32	96	720	1200
Visages	10 triangles	32 triangles	24 carrés	96 triangles	1200 triangles	720 pentagones
Cellules	5 tétraèdres	16 tétraèdres	8 cubes	24 octaèdres	600 tétraèdres	120 dodécaèdres
Rayon long	1	1	1	1	1	1
Longueur du bord	√ 5/√ 2 1.581	√ 2 ≈ 1,414	1	1	1/?? 0,618	1/√ 2 φ 2 0,270
Rayon court	1/4	1/2	1/2	√ 2/2 0,707	1 - (√ 2/2 √ 3 φ) 2 0,936	1 - (1/2 √ 3 φ) 2 0,968
Zone	dix•√ 8/3 9.428	32•√ 3/4 13.856	24	96•√ 3/4 41.569	1200•√ 3/8φ 2 99.238	720•25 + 10 √ 5/8φ 4 621,9
Le volume	5•5 √ 5/24 2.329	16•1/3 5.333	8	24•√ 2/3 11.314	600•1/3 √ 8 φ 3 16.693	120•2 + φ/2 √ 8 φ 3 18.118
4-Contenu	√ 5/24•(√ 5/2) 4 0,146	2/3 0,667	1	2	Court∙Vol/4 3.907	Court∙Vol/4 4.385

Le pentachore (5 cellules) est le plus simple des 9 polychores uniformes construits à partir du [3,3,3] groupe de Coxeter .

Schläfli	{3,3,3}	t{3,3,3}	r{3,3,3}	rr{3,3,3}	2t{3,3,3}	tr{3,3,3}	t 0,3 {3,3,3}	t 0,1,3 {3,3,3}	t 0,1,2,3 {3,3,3}
Coxeter
Schlegel

1 k2 chiffres en n dimensions
Espacer	Fini						euclidien	Hyperbolique
m	3	4	5	6	7	8	9	dix
Groupe Coxeter	E 3 =A 2 A 1	E 4 = A 4	E 5 = D 5	E 6	E 7	E 8	E 9 = = E 8 +${\displaystyle {\tilde {E}}_{8}}$	E 10 = = E 8 ++${\displaystyle {\bar {T}}_{8}}$
Diagramme de Coxeter
Symétrie (ordre)	[3 -1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[[3 2,2,1 ]]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Commander	12	120	1 920	103 680	2 903 040	696 729 600	??
Graphique							-	-
Nom	1 −1,2	1 02	1 12	1 22	1 32	1 42	1 52	1 62

2 k 1 chiffres en n dimensions
Espacer	Fini						euclidien	Hyperbolique
m	3	4	5	6	7	8	9	dix
Groupe Coxeter	E 3 =A 2 A 1	E 4 = A 4	E 5 = D 5	E 6	E 7	E 8	E 9 = = E 8 +${\displaystyle {\tilde {E}}_{8}}$	E 10 = = E 8 ++${\displaystyle {\bar {T}}_{8}}$
Diagramme de Coxeter
Symétrie	[3 -1,2,1 ]	[3 0,2,1 ]	[[3 1,2,1 ]]	[3 2,2,1 ]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Commander	12	120	384	51 840	2 903 040	696 729 600	??
Graphique							-	-
Nom	2 −1,1	2 01	2 11	2 21	2 31	2 41	2 51	2 61

Il est dans la séquence des polychores réguliers : le tesseract {4,3,3}, à 120 cellules {5,3,3}, de l'espace euclidien à 4, et le pavage hexagonal en nid d'abeille {6,3,3} de l'espace hyperbolique . Tous ont une figure de sommet tétraédrique .

{p,3,3} polytopes
Espacer		S 3			H 3
Former		Fini			Paracompacte	Non compact
Nom		{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	... {∞,3,3}
Image
Cellules {p,3}		{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

C'est l'un des trois polytopes réguliers à 4 cellules tétraédriques, avec les 16 cellules {3,3,4}, 600 cellules {3,3,5}. Le nid d'abeille tétraédrique d'ordre 6 {3,3,6} de l'espace hyperbolique a également des cellules tétraédriques.

{3,3,p} polytopes
Espacer	S 3			H 3
Former	Fini			Paracompacte	Non compact
Nom	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Image
Figure de sommet	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

{3, p ,3} polytopes
Espacer	S 3		H 3
Former	Fini		Compact	Paracompacte	Non compact
{3, p ,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Image
Cellules	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Figure de sommet	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{p,3,p} nids d'abeilles réguliers
Espacer	S 3	Euclidien E 3	H 3
Former	Fini	Affine	Compact	Paracompacte	Non compact
Nom	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	... {∞,3,∞}
Image
Cellules	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Figure de sommet	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Citations

Les références

• T. Gosset : Sur les figures régulières et semi-régulières dans l'espace à n dimensions , Messenger of Mathematics, Macmillan, 1900
• HSM Coxeter :
  • Coxeter, HSM (1973). Polytopes réguliers (3e éd.). New York : Douvres.
    • p. 120, §7.2. voir illustration Fig 7.2 A
    • p. 296, Tableau I (iii) : Polytopes réguliers, trois polytopes réguliers en n dimensions (n≥5)
  • Coxeter, HSM (1991), Regular Complex Polytopes (2e éd.), Cambridge: Cambridge University Press
  • Kaleidoscopes: Selected Writings of HSM Coxeter , édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Article 22) HSM Coxeter, Polytopes réguliers et semi-réguliers I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Document 23) HSM Coxeter, Polytopes réguliers et semi-réguliers II , [Math. Zeit. 188 (1985) 559-591]
    • (Document 24) HSM Coxeter, Polytopes réguliers et semi-réguliers III , [Math. Zeit. 200 (1988) 3-45]
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN  978-1-56881-220-5 (Chapitre 26. pp. 409 : Hemicubes : 1 _n1 )
• Norman Johnson Uniform Polytopes , Manuscrit (1991)
  • NW Johnson: La théorie des polytopes et nids d'abeilles uniformes , Ph.D. (1966)

Liens externes

• Weisstein, Eric W. "Pentatope" . MathWorld .
• Olchevski, Georges. "Pentachore" . Glossaire de l'hyperespace . Archivé de l'original le 4 février 2007.
  • 1. Polychore uniforme convexe basée sur le pentachore - Modèle 1 , George Olshevsky.
• Klitzing, Richard. "Polytopes uniformes 4D (polychora) x3o3o3o - stylo" .
• Der 5-Zeller (5-cell) Polytopes réguliers de Marco Möller dans R ⁴ (allemand)
• Jonathan Bowers, polychore régulière
• Applets Java3D
• pyrochore