Espace vectoriel - Vector space
Un espace vectoriel (également appelé espace linéaire ) est une collection d'objets appelés vecteurs , qui peuvent être additionnés et multipliés («mis à l'échelle») par des nombres, appelés scalaires . Les scalaires sont souvent considérés comme des nombres réels , mais il existe également des espaces vectoriels avec multiplication scalaire par des nombres complexes , des nombres rationnels ou généralement n'importe quel champ . Les opérations d'addition de vecteurs et de multiplication scalaire doivent satisfaire à certaines exigences, appelées axiomes vectoriels (listées ci-dessous au § Définition ). Pour spécifier que les scalaires sont des nombres réels ou complexes, les termes espace vectoriel réel et espace vectoriel complexe sont souvent utilisés.
Certains ensembles de vecteurs euclidiens sont des exemples courants d'espace vectoriel. Ils représentent des quantités physiques telles que des forces , où deux forces quelconques (du même type) peuvent être ajoutées pour en donner une troisième, et la multiplication d'un vecteur de force par un multiplicateur réel est un autre vecteur de force. Dans le même ordre d'idées (mais dans un sens plus géométrique ), les vecteurs représentant les déplacements dans le plan ou l' espace tridimensionnel forment également des espaces vectoriels. Les vecteurs dans les espaces vectoriels ne doivent pas nécessairement être des objets en forme de flèche comme ils apparaissent dans les exemples mentionnés: les vecteurs sont considérés comme des objets mathématiques abstraits avec des propriétés particulières, qui dans certains cas peuvent être visualisés sous forme de flèches.
Les espaces vectoriels font l'objet de l'algèbre linéaire et sont bien caractérisés par leur dimension qui, en gros, spécifie le nombre de directions indépendantes dans l'espace. Les espaces vectoriels de dimension infinie apparaissent naturellement dans l'analyse mathématique en tant qu'espaces de fonctions , dont les vecteurs sont des fonctions . Ces espaces vectoriels sont généralement dotés d'une structure supplémentaire telle qu'une topologie , ce qui permet de prendre en compte les problèmes de proximité et de continuité . Parmi ces topologies, celles qui sont définies par une norme ou un produit interne sont plus couramment utilisées (étant équipées d'une notion de distance entre deux vecteurs). C'est notamment le cas des espaces de Banach et des espaces de Hilbert , qui sont fondamentaux en analyse mathématique.
Historiquement, les premières idées menant aux espaces vectoriels remontent à la géométrie analytique du 17ème siècle , aux matrices , aux systèmes d' équations linéaires et aux vecteurs euclidiens. Le traitement moderne et plus abstrait, formulé pour la première fois par Giuseppe Peano en 1888, englobe des objets plus généraux que l' espace euclidien , mais une grande partie de la théorie peut être considérée comme une extension des idées géométriques classiques comme les lignes , les plans et leurs analogues de plus haute dimension.
Aujourd'hui, les espaces vectoriels sont appliqués à travers les mathématiques , la science et l' ingénierie . Ils sont la notion linéaire-algébrique appropriée pour traiter les systèmes d'équations linéaires . Ils offrent un cadre pour l'expansion de Fourier , qui est utilisé dans les routines de compression d'image , et ils fournissent un environnement qui peut être utilisé pour les techniques de résolution d' équations aux dérivées partielles . De plus, les espaces vectoriels fournissent une manière abstraite et sans coordonnées de traiter les objets géométriques et physiques tels que les tenseurs . Cela permet à son tour l'examen des propriétés locales des variétés par des techniques de linéarisation. Les espaces vectoriels peuvent être généralisés de plusieurs manières, conduisant à des notions plus avancées en géométrie et en algèbre abstraite .
| Structures algébriques |
|---|
Introduction et définition
Le concept d'espace vectoriel sera d'abord expliqué en décrivant deux exemples particuliers:
Premier exemple: flèches dans le plan
Le premier exemple d'espace vectoriel est constitué de flèches dans un plan fixe , commençant à un point fixe. Ceci est utilisé en physique pour décrire les forces ou les vitesses . Étant donné deux de ces flèches, v et w , le parallélogramme couvert par ces deux flèches contient une flèche diagonale qui commence également à l'origine. Cette nouvelle flèche est appelée la somme des deux flèches, et est notée v + w . Dans le cas particulier de deux flèches sur la même ligne, leur somme est la flèche sur cette ligne dont la longueur est la somme ou la différence des longueurs, selon que les flèches ont le même sens. Une autre opération qui peut être effectuée avec des flèches est la mise à l'échelle: étant donné tout nombre réel positif a , la flèche qui a la même direction que v , mais qui est dilatée ou rétrécie en multipliant sa longueur par a , est appelée multiplication de v par a . Il est noté un v . Quand a est négatif, un v est défini comme la flèche pointant dans la direction opposée à la place.
Ce qui suit montre quelques exemples: si a = 2 , le vecteur résultant a w a la même direction que w , mais est étiré à la double longueur de w (image de droite ci-dessous). De manière équivalente, 2 w est la somme w + w . De plus, (−1) v = - v a la direction opposée et la même longueur que v (vecteur bleu pointant vers le bas dans l'image de droite).

|
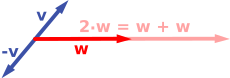
|
Deuxième exemple: paires ordonnées de nombres
Un deuxième exemple clé d'un espace vectoriel est fourni par des paires de nombres réels x et y . (L'ordre des composantes x et y est significatif, donc une telle paire est également appelée paire ordonnée .) Une telle paire s'écrit ( x , y ) . La somme de deux de ces paires et la multiplication d'une paire par un nombre sont définies comme suit:
- ( x 1 , y 1 ) + ( x 2 , y 2 ) = ( x 1 + x 2 , y 1 + y 2 )
et
- a ( x , y ) = ( ax , ay ) .
Le premier exemple ci-dessus se réduit à celui-ci, si les flèches sont représentées par la paire de coordonnées cartésiennes de leurs extrémités.
Définition
Dans cet article, les vecteurs sont représentés en gras pour les distinguer des scalaires.
Un espace vectoriel sur un champ F est un ensemble V avec deux opérations qui satisfont les huit axiomes listés ci-dessous. Dans ce qui suit, V × V désigne le produit cartésien de V avec lui-même, et → désigne une application d'un ensemble à un autre.
- La première opération, appelée addition de vecteurs ou simplement addition +: V × V → V , prend deux vecteurs v et w quelconques et leur assigne un troisième vecteur qui s'écrit couramment v + w , et appelé la somme de ces deux vecteurs. (Le vecteur résultant est également un élément de l'ensemble V. )
- La seconde opération, appelée multiplication scalaire ·: F × V → V, prend tout scalaire a et tout vecteur v et donne un autre vecteur a v . (De même, le vecteur a v est un élément de l'ensemble V. La multiplication scalaire ne doit pas être confondue avec le produit scalaire , également appelé produit interne ou produit scalaire , qui est une structure supplémentaire présente sur certains espaces vectoriels spécifiques, mais pas tous . La multiplication scalaire est une multiplication d'un vecteur par un scalaire; l'autre est une multiplication de deux vecteurs produisant un scalaire.)
Les éléments de V sont communément appelés vecteurs . Les éléments de F sont communément appelés scalaires . Les symboles courants pour désigner les espaces vectoriels incluent , et .
Dans les deux exemples ci-dessus, le champ est le champ des nombres réels, et l'ensemble des vecteurs se compose des flèches planes avec un point de départ fixe et des paires de nombres réels, respectivement.
Pour être qualifié d'espace vectoriel, l'ensemble V et les opérations d'addition et de multiplication doivent respecter un certain nombre d'exigences appelées axiomes . Ceux - ci sont énumérés dans le tableau ci - dessous, où u , v et w désignent des vecteurs arbitraires en V , et a et b représentent des valeurs scalaires dans F .
| Axiome | Sens |
|---|---|
| Associativité de l'addition | u + ( v + w ) = ( u + v ) + w |
| Commutativité de l'addition | u + v = v + u |
| Élément d'identité de l'addition | Il existe un élément 0 ∈ V , appelé le vecteur nul , tel que v + 0 = v pour tout v ∈ V . |
| Éléments d'addition inverses | Pour tout v ∈ V , il existe un élément - v ∈ V , appelé l' inverse additif de v , tel que v + (- v ) = 0 . |
| Compatibilité de la multiplication scalaire avec la multiplication de champ | a ( b v ) = ( ab ) v |
| Élément d'identité de la multiplication scalaire | 1 v = v , où 1 désigne l' identité multiplicative dans F . |
| Distributivité de la multiplication scalaire par rapport à l'addition vectorielle | a ( u + v ) = a u + a v |
| Distributivité de la multiplication scalaire par rapport à l'addition de champ | ( a + b ) v = a v + b v |
Ces axiomes généralisent les propriétés des vecteurs introduits dans les exemples ci-dessus. En effet, le résultat de l'addition de deux paires ordonnées (comme dans le deuxième exemple ci-dessus) ne dépend pas de l'ordre des sommations:
- ( x v , y v ) + ( x w , y w ) = ( x w , y w ) + ( x v , y v ) .
De même, dans l'exemple géométrique des vecteurs sous forme de flèches, v + w = w + v puisque le parallélogramme définissant la somme des vecteurs est indépendant de l'ordre des vecteurs. Tous les autres axiomes peuvent être vérifiés de la même manière dans les deux exemples. Ainsi, en ne tenant pas compte de la nature concrète du type particulier de vecteurs, la définition incorpore ces deux exemples et bien d'autres dans une notion d'espace vectoriel.
La soustraction de deux vecteurs et la division par un scalaire (non nul) peut être définie comme
- .
Lorsque le champ scalaire F correspond aux nombres réels R , l'espace vectoriel est appelé espace vectoriel réel . Lorsque le champ scalaire correspond aux nombres complexes C , l'espace vectoriel est appelé un espace vectoriel complexe . Ces deux cas sont ceux utilisés le plus souvent en ingénierie. La définition générale d'un espace vectoriel permet scalaires comme des éléments d' une quelconque fixe champ F . La notion est alors connu comme un F - espace vectoriel ou un espace vectoriel sur F . Un champ est, essentiellement, un ensemble de nombres possédant des opérations d' addition , de soustraction , de multiplication et de division . Par exemple, les nombres rationnels forment un champ.
Contrairement à l'intuition issue des vecteurs dans le plan et les cas de plus haute dimension, dans les espaces vectoriels généraux, il n'y a pas de notion de proximité , d' angles ou de distances . Pour traiter ces questions, des types particuliers d'espaces vectoriels sont introduits; voir § Espaces vectoriels avec structure supplémentaire ci-dessous pour plus d'informations.
Formulations alternatives et conséquences élémentaires
Addition vectorielle et une multiplication scalaire sont des opérations, répondant à la fermeture du logement: u + v et un v sont en V pour toutes un en F , et u , v dans V . Certaines sources plus anciennes mentionnent ces propriétés comme des axiomes séparés.
Dans le langage de l'algèbre abstraite , les quatre premiers axiomes sont équivalents à exiger que l'ensemble des vecteurs soit un groupe abélien sous addition. Les axiomes donnent à ce groupe un F - module de structure. En d'autres termes, il existe un homomorphisme en anneau f du champ F dans l' anneau d'endomorphisme du groupe de vecteurs. Alors la multiplication scalaire a v est définie comme ( f ( a )) ( v ) .
Il existe un certain nombre de conséquences directes des axiomes de l'espace vectoriel. Certains d'entre eux dérivent de la théorie élémentaire des groupes , appliquée au groupe additif de vecteurs: par exemple, le vecteur nul 0 de V et l'inverse additif - v de tout vecteur v sont uniques. D'autres propriétés suivent en employant également la loi de distribution pour la multiplication scalaire, par exemple a v vaut 0 si et seulement si a vaut 0 ou v vaut 0 .
Histoire
Les espaces vectoriels proviennent de la géométrie affine , via l'introduction de coordonnées dans le plan ou dans l'espace tridimensionnel. Vers 1636, les mathématiciens français René Descartes et Pierre de Fermat fondèrent la géométrie analytique en identifiant des solutions à une équation de deux variables avec des points sur une courbe plane . Pour obtenir des solutions géométriques sans utiliser de coordonnées, Bolzano a introduit, en 1804, certaines opérations sur les points, les lignes et les plans, qui sont les prédécesseurs des vecteurs. Ce travail a été utilisé dans la conception des coordonnées barycentriques par Möbius en 1827. Le fondement de la définition des vecteurs était la notion de Bellavitis du bipoint, un segment orienté dont l'une des extrémités est l'origine et l'autre une cible. Les vecteurs ont été reconsidérés avec la présentation des nombres complexes par Argand et Hamilton et la création de quaternions par ce dernier. Ce sont des éléments en R 2 et R 4 ; les traiter à l'aide de combinaisons linéaires remonte à Laguerre en 1867, qui définissait également des systèmes d'équations linéaires .
En 1857, Cayley a introduit la notation matricielle qui permet une harmonisation et une simplification des cartes linéaires . Vers la même époque, Grassmann a étudié le calcul barycentrique initié par Möbius. Il envisage des ensembles d'objets abstraits dotés d'opérations. Dans son travail, les concepts d' indépendance et de dimension linéaires , ainsi que les produits scalaires sont présents. En fait, le travail de Grassmann en 1844 dépasse le cadre des espaces vectoriels, car sa réflexion sur la multiplication l'a également conduit à ce que l'on appelle aujourd'hui les algèbres . Le mathématicien italien Peano a été le premier à donner la définition moderne des espaces vectoriels et des cartes linéaires en 1888.
Un développement important des espaces vectoriels est dû à la construction des espaces fonctionnels par Henri Lebesgue . Cela a ensuite été formalisé par Banach et Hilbert , vers 1920. À cette époque, l' algèbre et le nouveau champ de l'analyse fonctionnelle ont commencé à interagir, notamment avec des concepts clés tels que les espaces de fonctions p- intégrables et les espaces de Hilbert . À cette époque également, les premières études concernant les espaces vectoriels de dimension infinie ont été effectuées.
Exemples
Coordonner l'espace
L'exemple le plus simple d'un espace vectoriel sur un champ F est le champ lui-même, équipé de son addition et de sa multiplication standard. Plus généralement, tous les n -tuples (séquences de longueur n )
- ( un 1 , un 2 , ..., un n )
des éléments de F forment un espace vectoriel qui est généralement noté F n et appelé espace de coordonnées . Le cas n = 1 est l'exemple le plus simple mentionné ci-dessus, dans lequel le champ F est également considéré comme un espace vectoriel sur lui-même. Le cas F = R et n = 2 a été discuté dans l'introduction ci-dessus.
Nombres complexes et autres extensions de champ
L'ensemble des nombres complexes C , c'est-à-dire les nombres qui peuvent être écrits sous la forme x + iy pour les nombres réels x et y où i est l' unité imaginaire , forment un espace vectoriel sur les réels avec l'addition et la multiplication habituelles: ( x + iy ) + ( a + ib ) = ( x + a ) + i ( y + b ) et c ⋅ ( x + iy ) = ( c ⋅ x ) + i ( c ⋅ y ) pour les nombres réels x , y , a , b et c . Les différents axiomes d'un espace vectoriel découlent du fait que les mêmes règles s'appliquent à l'arithmétique des nombres complexes.
En fait, l'exemple des nombres complexes est essentiellement le même (c'est-à-dire qu'il est isomorphe ) à l'espace vectoriel des paires ordonnées de nombres réels mentionné ci-dessus: si nous considérons le nombre complexe x + i y comme représentant la paire ordonnée ( x , y ) dans le plan complexe alors on voit que les règles d'addition et de multiplication scalaire correspondent exactement à celles de l'exemple précédent.
De manière plus générale, les extensions de terrain fournissent une autre classe d'exemples d'espaces vectoriels, en particulier en algèbre et théorie algébrique des nombres : un champ F contenant un plus petit champ E est un E espace -vector, par les opérations de multiplication et d' addition donnés de F . Par exemple, les nombres complexes sont un espace vectoriel sur R , et l'extension de champ est un espace vectoriel sur Q .
Espaces fonctionnels
Les fonctions de tout ensemble fixe Ω vers un champ F forment également des espaces vectoriels, en effectuant une addition et une multiplication scalaire point par point. Autrement dit, la somme de deux fonctions f et g est la fonction ( f + g ) donnée par
- ( f + g ) ( w ) = f ( w ) + g ( w ) ,
et de même pour la multiplication. De tels espaces fonctionnels se produisent dans de nombreuses situations géométriques, lorsque Ω est la ligne réelle ou un intervalle , ou d' autres sous - ensembles de R . De nombreuses notions de topologie et d'analyse, telles que la continuité , l' intégrabilité ou la différentiabilité se comportent bien en ce qui concerne la linéarité: les sommes et les multiples scalaires de fonctions possédant une telle propriété ont toujours cette propriété. Par conséquent, l'ensemble de ces fonctions sont des espaces vectoriels. Ils sont étudiés plus en détail à l'aide des méthodes d' analyse fonctionnelle , voir ci - dessous . Les contraintes algébriques donnent également des espaces vectoriels: l' espace vectoriel F [x] est donné par des fonctions polynomiales :
- f ( x ) = r 0 + r 1 x + ... + r n -1 x n -1 + r n x n , où les coefficients r 0 , ..., r n sont F .
Équations linéaires
Les systèmes d' équations linéaires homogènes sont étroitement liés aux espaces vectoriels. Par exemple, les solutions de
une + 3 b + c = 0 4 un + 2 b + 2 c = 0
sont donnés par des triplets avec a , b = a / 2 et c = −5 a / 2 arbitraires . Ils forment un espace vectoriel: les sommes et les multiples scalaires de ces triplets satisfont toujours aux mêmes rapports des trois variables; ce sont donc aussi des solutions. Les matrices peuvent être utilisées pour condenser plusieurs équations linéaires comme ci-dessus en une seule équation vectorielle, à savoir
- Un x = 0 ,
où A = est la matrice contenant les coefficients des équations données, x est le vecteur ( a , b , c ) , A x désigne le produit de la matrice et 0 = (0, 0) est le vecteur nul. Dans la même veine, les solutions d' équations différentielles linéaires homogènes forment des espaces vectoriels. Par exemple,
- f ′ ′ ( x ) + 2 f ′ ( x ) + f ( x ) = 0
donne f ( x ) = a e - x + bx e - x , où a et b sont des constantes arbitraires, et e x est la fonction exponentielle naturelle .
Base et dimension

Les bases permettent de représenter des vecteurs par une séquence de scalaires appelés coordonnées ou composants . Une base est un ensemble (fini ou infini) B = { b i } i ∈ I de vecteurs b i , souvent indexé par un ensemble d'indices I , qui couvre tout l'espace et est linéairement indépendant . "Couvrant tout l'espace" signifie que tout vecteur v peut être exprimé comme une somme finie (appelée combinaison linéaire ) des éléments de base:
-
( 1 )
où l' un k sont des scalaires, appelés les coordonnées (ou les composants) du vecteur v par rapport à la base B , et b i k ( k = 1, ..., n ) éléments de B . L'indépendance linéaire signifie que les coordonnées a k sont déterminées de manière unique pour n'importe quel vecteur dans l'espace vectoriel.
Par exemple, les vecteurs de coordonnées e 1 = (1, 0, ..., 0) , e 2 = (0, 1, 0, ..., 0) , to e n = (0, 0, ... , 0, 1) , forment une base de F n , appelée base standard , puisque tout vecteur ( x 1 , x 2 , ..., x n ) peut être exprimé de manière unique comme une combinaison linéaire de ces vecteurs:
- ( x 1 , x 2 , ..., x n ) = x 1 (1, 0, ..., 0) + x 2 (0, 1, 0, ..., 0) + ... + x n (0, ..., 0, 1) = x 1 e 1 + x 2 e 2 + ... + x n e n .
Les coordonnées correspondantes x 1 , x 2 , ... , x n ne sont que les coordonnées cartésiennes du vecteur.
Chaque espace vectoriel a une base. Cela découle du lemme de Zorn , une formulation équivalente de l' axiome du choix . Étant donné les autres axiomes de la théorie des ensembles de Zermelo – Fraenkel , l'existence de bases équivaut à l'axiome du choix. Le lemme de l'ultrafiltre , qui est plus faible que l'axiome de choix, implique que toutes les bases d'un espace vectoriel donné ont le même nombre d'éléments, ou cardinalité (cf. Théorème de dimension pour les espaces vectoriels ). Elle est appelée la dimension de l'espace vectoriel, notée dim V . Si l'espace est couvert par un nombre fini de vecteurs, les déclarations ci-dessus peuvent être prouvées sans une telle contribution fondamentale de la théorie des ensembles.
La dimension de l'espace de coordonnées F n est n , par la base exposée ci-dessus. La dimension de l'anneau polynomial F [ x ] introduit ci - dessus est dénombrable infinie , une base est donnée par 1 , x , x 2 , ... A fortiori , la dimension des espaces fonctionnels plus généraux, comme l'espace des fonctions sur certains (borné ou illimité), est infini. Sous des hypothèses de régularité appropriées sur les coefficients impliqués, la dimension de l'espace de solution d'une équation différentielle ordinaire homogène est égale au degré de l'équation. Par exemple, l'espace de solution pour l' équation ci - dessus est généré par e - x et xe - x . Ces deux fonctions sont linéairement indépendantes sur R , donc la dimension de cet espace est de deux, tout comme le degré de l'équation.
Une extension de champ sur les rationnels Q peut être considérée comme un espace vectoriel sur Q (en définissant l'addition de vecteur comme addition de champ, en définissant la multiplication scalaire comme multiplication de champ par des éléments de Q , et en ignorant autrement la multiplication de champ). La dimension (ou degré ) de l'extension de champ Q (α) sur Q dépend de α . Si α satisfait une équation polynomiale
Cartes et matrices linéaires
La relation de deux espaces vectoriels peut être exprimée par une carte linéaire ou une transformation linéaire . Ce sont des fonctions qui reflètent la structure de l'espace vectoriel, c'est-à-dire qu'elles préservent les sommes et la multiplication scalaire:
- et f ( a · v ) un · f ( v ) pour tous les v et w dans V , tous les un à F .
Un isomorphisme est une application linéaire f : V → W telle qu'il existe une application inverse g : W → V , qui est une application telle que les deux compositions possibles f ∘ g : W → W et g ∘ f : V → V sont cartes d'identité . De manière équivalente, f est à la fois un-à-un ( injectif ) et sur ( surjectif ). S'il existe un isomorphisme entre V et W , les deux espaces sont dits isomorphes ; ils sont alors essentiellement identiques aux espaces vectoriels, puisque toutes les identités tenant dans V sont, via f , transportées vers des identités similaires dans W , et vice versa via g .
Par exemple, les espaces vectoriels «flèches dans le plan» et «paires ordonnées de nombres» dans l'introduction sont isomorphes: une flèche plane v partant à l' origine d'un système de coordonnées (fixe) peut être exprimée comme une paire ordonnée en considérant le x - et y - composants de la flèche, comme indiqué dans l'image à droite. Inversement, étant donné une paire ( x , y ) , la flèche allant de x vers la droite (ou vers la gauche, si x est négatif), et y vers le haut (vers le bas, si y est négatif) fait reculer la flèche v .
Les applications linéaires V → W entre deux espaces vectoriels forment un espace vectoriel Hom F ( V , W ) , également noté L ( V , W ) . L'espace des applications linéaires de V à F est appelé espace vectoriel dual , noté V ∗ . Via la carte naturelle injective V → V ∗∗ , tout espace vectoriel peut être intégré dans son biduel ; la carte est un isomorphisme si et seulement si l'espace est de dimension finie.
Une fois qu'une base de V est choisie, les cartes linéaires f : V → W sont complètement déterminées en spécifiant les images des vecteurs de base, car tout élément de V est exprimé uniquement comme une combinaison linéaire de ceux-ci. Si dim V = dim W , un 1-à-1 correspondance entre les bases fixes de V et W donne lieu à une application linéaire qui fait correspondre un élément de base de V à l'élément de base correspondant de W . C'est un isomorphisme, par sa définition même. Par conséquent, deux espaces vectoriels sont isomorphes si leurs dimensions concordent et vice versa. Une autre façon d'exprimer cela est que tout espace vectoriel est complètement classé ( jusqu'à l' isomorphisme) par sa dimension, un seul nombre. En particulier, tout espace vectoriel F à n dimensions V est isomorphe à F n . Il n'y a cependant pas d'isomorphisme «canonique» ou préféré; en fait un isomorphisme φ : F n → V équivaut au choix d'une base de V , en mappant la base standard de F n à V , via φ . La liberté de choisir une base convenable est particulièrement utile dans le contexte de dimension infinie; voir ci - dessous .
Matrices
Les matrices sont une notion utile pour encoder des cartes linéaires. Ils sont écrits sous la forme d'un tableau rectangulaire de scalaires comme dans l'image de droite. Toute matrice m -by- n A donne lieu à une application linéaire de F n à F m , de la façon suivante
- , où désigne la somme ,
ou, en utilisant la multiplication matricielle de la matrice A avec le vecteur de coordonnées x :
- x ↦ A x .
De plus, après avoir choisi les bases de V et W , toute application linéaire f : V → W est représentée uniquement par une matrice via cette affectation.
Le déterminant det ( A ) d'une matrice carrée A est un scalaire qui indique si l'application associée est un isomorphisme ou non: pour être ainsi, il suffit et nécessaire que le déterminant soit non nul. La transformation linéaire de R n correspondant à une matrice n -by- n réelle est une orientation préservant si et seulement si son déterminant est positif.
Valeurs propres et vecteurs propres
Les endomorphismes , applications linéaires f : V → V , sont particulièrement importants puisque dans ce cas les vecteurs v peuvent être comparés à leur image sous f , f ( v ) . Tout vecteur v différent de zéro satisfaisant λ v = f ( v ) , où λ est un scalaire, est appelé un vecteur propre de f de valeur propre λ . De manière équivalente, v est un élément du noyau de la différence f - λ · Id (où Id est la carte d'identité V → V ) . Si V est de dimension finie, cela peut être reformulé en utilisant des déterminants: f ayant une valeur propre λ équivaut à
- det ( f - λ · Id) = 0 .
En épelant la définition du déterminant, l'expression sur le côté gauche peut être considérée comme une fonction polynomiale en λ , appelée polynôme caractéristique de f . Si le champ F est suffisamment grand pour contenir un zéro de ce polynôme (ce qui se produit automatiquement pour F algébriquement fermé , tel que F = C ) toute application linéaire a au moins un vecteur propre. L'espace vectoriel V peut posséder ou non une base propre , une base constituée de vecteurs propres. Ce phénomène est régi par la forme canonique jordanienne de la carte. L'ensemble de tous les vecteurs propres correspondant à une valeur propre particulière de f forme un espace vectoriel appelé espace propre correspondant à la valeur propre (et f ) en question. Pour atteindre le théorème spectral , l'énoncé correspondant dans le cas de dimension infinie, la machinerie de l'analyse fonctionnelle est nécessaire, voir ci - dessous .
Constructions de base
En plus des exemples concrets ci-dessus, il existe un certain nombre de constructions algébriques linéaires standard qui donnent des espaces vectoriels liés à ceux donnés. En plus des définitions données ci-dessous, ils sont également caractérisés par des propriétés universelles , qui déterminent un objet X en spécifiant les cartes linéaires de X à tout autre espace vectoriel.
Sous-espaces et espaces de quotient
Un sous- ensemble non vide W d'un espace vectoriel V qui est fermé sous addition et multiplication scalaire (et contient donc le 0 -vecteur de V ) est appelé un sous - espace linéaire de V , ou simplement un sous - espace de V , lorsque l'espace ambiant est sans ambiguïté un espace vectoriel. Les sous -espaces de V sont des espaces vectoriels (sur le même champ) à part entière. L'intersection de tous les sous - espaces contenant un ensemble S de vecteurs est appelé sa durée , et il est le plus petit sous - espace de V contenant l'ensemble S . Exprimé en termes d'éléments, la portée est le sous - espace constitué par l' ensemble des combinaisons linéaires des éléments de S .
Un sous-espace linéaire de dimension 1 est une ligne vectorielle . Un sous-espace linéaire de dimension 2 est un plan vectoriel . Un sous-espace linéaire qui contient tous les éléments sauf l'un d'une base de l'espace ambiant est un hyperplan vectoriel . Dans un espace vectoriel de dimension finie n , un hyperplan vectoriel est donc un sous-espace de dimension n - 1 .
La contrepartie des sous-espaces sont les espaces vectoriels quotients . Compte tenu de tout sous - espace W ⊂ V , l'espace quotient V / W ( " V modulo W est défini") comme suit: comme un ensemble, il se compose de v + W = { v + w : w ∈ W }, où v est un vecteur arbitraire V . La somme de deux tels éléments v 1 + W et v 2 + W est ( v 1 + v 2 ) + W , et la multiplication scalaire est donnée par un · ( v + W ) = ( a · v ) + W . Le point clé de cette définition est que v 1 + W = v 2 + W si et seulement si la différence de v 1 et v 2 réside dans W . De cette façon, l'espace quotient informations « de oublie » qui est contenue dans le sous - espace W .
Le noyau ker ( f ) d'une carte linéaire f : V → W est constituée de vecteurs v qui sont mis en correspondance avec 0 à W . Le noyau et l' image im ( f ) = { f ( v ): v ∈ V } sont des sous-espaces de V et W , respectivement. L'existence de noyaux et d'images fait partie de l'affirmation selon laquelle la catégorie des espaces vectoriels (sur un champ fixe F ) est une catégorie abélienne , c'est-à-dire un corpus d'objets mathématiques et des cartes de préservation de la structure entre eux (une catégorie ) qui se comporte un peu comme la catégorie des groupes abéliens . Pour cette raison, de nombreuses déclarations telles que le premier théorème d'isomorphisme (également appelé théorème de rang-nullité en termes liés à la matrice)
- V / ker ( f ) ≡ im ( f ).
et les deuxième et troisième théorèmes d'isomorphisme peuvent être formulés et prouvés d'une manière très similaire aux déclarations correspondantes pour les groupes .
Un exemple important est le noyau d'une application linéaire x ↦ A x pour une matrice fixe A , comme ci-dessus . Le noyau de cette carte est le sous - espace de vecteurs x tels que A x = 0 , ce qui est précisément l'ensemble des solutions du système d'équations linéaires homogènes appartenant à A . Ce concept s'étend également aux équations différentielles linéaires
- , où les coefficients a i sont également des fonctions dans x .
Dans la carte correspondante
- ,
les dérivées de la fonction f apparaissent linéairement (par opposition à f '' ( x ) 2 , par exemple). Puisque la différenciation est une procédure linéaire (c'est-à-dire ( f + g ) ′ = f ′ + g ′ et ( c · f ) ′ = c · f ′ pour une constante c ), cette affectation est linéaire, appelée opérateur différentiel linéaire . En particulier, les solutions de l'équation différentielle D ( f ) = 0 forment un espace vectoriel (sur R ou C ).
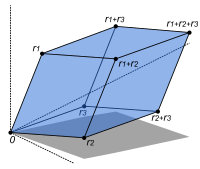
Produit direct et somme directe
Le produit direct des espaces vectoriels et la somme directe des espaces vectoriels sont deux manières de combiner une famille indexée d'espaces vectoriels dans un nouvel espace vectoriel.
Le produit direct d'une famille d'espaces vectoriels V i consiste en l'ensemble de tous les tuples ( v i ) i ∈ I , qui spécifient pour chaque indice i dans un ensemble d'indices I un élément v i de V i . L'addition et la multiplication scalaire sont effectuées par composants. Une variante de cette construction est la somme directe (également appelée coproduit et notée ), où seuls les tuples avec un nombre fini de vecteurs non nuls sont autorisés. Si l'ensemble d'indices I est fini, les deux constructions concordent, mais en général elles sont différentes.
Produit tensoriel
Le produit tensoriel V ⊗ F W , ou simplement V ⊗ W , de deux espaces vectoriels V et W est l'une des notions centrales de l' algèbre multilinéaire qui traite de l'extension de notions telles que les applications linéaires à plusieurs variables. Une application g : V × W → X est dite bilinéaire si g est linéaire dans les deux variables v et w . C'est-à-dire que pour w fixe l'application v ↦ g ( v , w ) est linéaire au sens ci-dessus et de même pour v fixe .
Le produit tensoriel est un espace vectoriel particulier qui est un destinataire universel des cartes bilinéaires g , comme suit. Il est défini comme l'espace vectoriel constitué de sommes finies (formelles) de symboles appelés tenseurs
- v 1 ⊗ w 1 + v 2 ⊗ w 2 + ... + v n ⊗ w n ,
soumis aux règles
- a · ( v ⊗ w ) = ( a · v ) ⊗ w = v ⊗ ( a · w ), où a est un scalaire,
- ( v 1 + v 2 ) ⊗ w = v 1 ⊗ w + v 2 ⊗ w , et
- v ⊗ ( w 1 + w 2 ) = v ⊗ w 1 + v ⊗ w 2 .

Ces règles garantissent que l'application f de V × W à V ⊗ W qui mappe un tuple ( v , w ) à v ⊗ w est bilinéaire. L'universalité stipule que, étant donné tout espace vectoriel X et toute application bilinéaire g : V × W → X , il existe une application unique u , représentée dans le diagramme avec une flèche en pointillé, dont la composition avec f est égale à g : u ( v ⊗ w ) = g ( v , w ) . C'est ce qu'on appelle la propriété universelle du produit tensoriel, une instance de la méthode - très utilisée dans l'algèbre abstraite avancée - pour définir indirectement des objets en spécifiant des cartes depuis ou vers cet objet.
Espaces vectoriels avec structure supplémentaire
Du point de vue de l'algèbre linéaire, les espaces vectoriels sont complètement compris dans la mesure où tout espace vectoriel est caractérisé, jusqu'à l'isomorphisme, par sa dimension. Cependant, les espaces vectoriels en soi n'offrent pas de cadre pour traiter la question - cruciale pour l'analyse - si une séquence de fonctions converge vers une autre fonction. De même, l'algèbre linéaire n'est pas adaptée pour traiter des séries infinies , puisque l'opération d'addition ne permet d'ajouter qu'un nombre fini de termes. Par conséquent, les besoins de l'analyse fonctionnelle nécessitent de considérer des structures supplémentaires.
Un espace vectoriel peut avoir un ordre partiel ≤, sous lequel certains vecteurs peuvent être comparés. Par exemple, l' espace réel à n dimensions R n peut être ordonné en comparant ses vecteurs par composants. Les espaces vectoriels ordonnés , par exemple les espaces de Riesz , sont fondamentaux pour l' intégration de Lebesgue , qui repose sur la capacité à exprimer une fonction comme une différence de deux fonctions positives
- f = f + - f - ,
où f + désigne la partie positive de f et f - la partie négative.
Espaces vectoriels normalisés et espaces intérieurs de produits
La "mesure" des vecteurs se fait en spécifiant une norme , une donnée qui mesure les longueurs des vecteurs, ou par un produit interne , qui mesure les angles entre les vecteurs. Les normes et les produits internes sont respectivement désignés et . La donnée d'un produit interne implique que les longueurs des vecteurs peuvent également être définies, en définissant la norme associée . Les espaces vectoriels dotés de telles données sont appelés respectivement espaces vectoriels normés et espaces de produit internes .
L'espace de coordonnées F n peut être équipé du produit scalaire standard :
Dans R 2 , cela reflète la notion commune d'angle entre deux vecteurs x et y , par la loi des cosinus :
Pour cette raison, deux vecteurs satisfaisants sont appelés orthogonaux . Une variante importante du produit scalaire standard est utilisée dans l'espace Minkowski : R 4 doté du produit Lorentz
Contrairement au produit scalaire standard, il n'est pas défini positif : prend également des valeurs négatives, par exemple pour . La distinction de la quatrième coordonnée - correspondant au temps , par opposition à trois dimensions spatiales - la rend utile pour le traitement mathématique de la relativité restreinte .
Espaces vectoriels topologiques
Les questions de convergence sont traitées en considérant des espaces vectoriels V portant une topologie compatible , une structure qui permet de parler d'éléments proches les uns des autres . Compatible ici signifie que l'addition et la multiplication scalaire doivent être des cartes continues . En gros, si x et y dans V , et a dans F varient d'un montant borné, il en va de même pour x + y et a x . Pour donner un sens à la spécification de la quantité de changement d'un scalaire, le champ F doit également porter une topologie dans ce contexte; un choix commun sont les réels ou les nombres complexes.
Dans de tels espaces vectoriels topologiques, on peut considérer des séries de vecteurs. La somme infinie
désigne la limite des sommes partielles finies correspondantes de la séquence ( f i ) i ∈ N d'éléments de V . Par exemple, les f i pourraient être des fonctions (réelles ou complexes) appartenant à un certain espace de fonctions V , auquel cas la série est une série de fonctions . Le mode de convergence de la série dépend de la topologie imposée à l'espace fonctionnel. Dans de tels cas, la convergence ponctuelle et la convergence uniforme sont deux exemples marquants.

Une manière d'assurer l'existence des limites de certaines séries infinies est de restreindre l'attention aux espaces où toute séquence de Cauchy a une limite; un tel espace vectoriel est appelé complet . En gros, un espace vectoriel est complet à condition qu'il contienne toutes les limites nécessaires. Par exemple, l'espace vectoriel des polynômes sur l'intervalle unitaire [0,1], équipé de la topologie de convergence uniforme n'est pas complet car toute fonction continue sur [0,1] peut être uniformément approchée par une suite de polynômes, par le Théorème d'approximation de Weierstrass . En revanche, l'espace de toutes les fonctions continues sur [0,1] avec la même topologie est complet. Une norme donne naissance à une topologie en définissant qu'une suite de vecteurs v n converge vers v si et seulement si
Les espaces de Banach et de Hilbert sont des espaces vectoriels topologiques complets dont les topologies sont données respectivement par une norme et un produit interne. Leur étude - un élément clé de l'analyse fonctionnelle - se concentre sur les espaces vectoriels de dimension infinie, puisque toutes les normes sur les espaces vectoriels topologiques de dimension finie donnent lieu à la même notion de convergence. L'image de droite montre l'équivalence de la norme 1 et de la norme ∞ sur R 2 : comme les «boules» unitaires se renferment, une séquence converge vers zéro dans une norme si et seulement si c'est le cas dans l'autre norme . Dans le cas des dimensions infinies, cependant, il y aura généralement des topologies inéquivalentes, ce qui rend l'étude des espaces vectoriels topologiques plus riche que celle des espaces vectoriels sans données supplémentaires.
D'un point de vue conceptuel, toutes les notions liées aux espaces vectoriels topologiques doivent correspondre à la topologie. Par exemple, au lieu de considérer toutes les cartes linéaires (également appelées fonctionnelles ) V → W , les cartes entre les espaces vectoriels topologiques doivent être continues. En particulier, l' espace dual (topologique) V ∗ est constitué de fonctionnelles continues V → R (ou vers C ). Le théorème fondamental de Hahn – Banach concerne la séparation des sous-espaces d'espaces vectoriels topologiques appropriés par des fonctionnelles continues.
Espaces Banach
Les espaces de Banach , introduits par Stefan Banach , sont des espaces vectoriels normés complets.
Un premier exemple est l'espace vectoriel constitué de vecteurs infinis avec des entrées réelles dont la -norm donnée par
- pour et .
Les topologies sur l'espace de dimension infinie sont inéquivalentes pour différentes . Par exemple, la séquence de vecteurs , dans laquelle se trouvent les premières composantes et les suivantes , converge vers le vecteur zéro pour , mais pas pour :
- , mais
Plus généralement que les suites de nombres réels, les fonctions sont dotées d'une norme qui remplace la somme ci-dessus par l' intégrale de Lebesgue
Les espaces de fonctions intégrables sur un domaine donné (par exemple un intervalle) satisfaisant , et équipés de cette norme sont appelés espaces de Lebesgue , notés .
Ces espaces sont complets. (Si l'on utilise à la place l' intégrale de Riemann , l'espace n'est pas complet, ce qui peut être vu comme une justification de la théorie d'intégration de Lebesgue.) Concrètement, cela signifie que pour toute suite de fonctions de Lebesgue intégrables avec , satisfaisant la condition
il existe une fonction appartenant à l'espace vectoriel telle que
Imposer des conditions de bornage non seulement sur la fonction, mais aussi sur ses dérivées conduit à des espaces de Sobolev .
Espaces Hilbert
Les espaces intérieurs complets des produits sont appelés espaces Hilbert , en l'honneur de David Hilbert . L'espace de Hilbert L 2 (Ω), avec produit interne donné par
où désigne le conjugué complexe de g ( x ), est un cas clé.
Par définition, dans un espace de Hilbert, toute séquence de Cauchy converge vers une limite. Inversement, trouver une séquence de fonctions f n avec des propriétés souhaitables qui se rapproche d'une fonction limite donnée est tout aussi crucial. Une première analyse, sous la forme de l' approximation de Taylor , a établi une approximation des fonctions différentiables f par polynômes. Par le théorème de Stone – Weierstrass , chaque fonction continue sur [ a , b ] peut être approchée aussi étroitement que souhaité par un polynôme. Une technique d'approximation similaire par fonctions trigonométriques est communément appelée expansion de Fourier et est très appliquée en ingénierie, voir ci - dessous . Plus généralement, et plus conceptuellement, le théorème donne une description simple de quelles «fonctions de base», ou, dans des espaces abstraits de Hilbert, quels vecteurs de base suffisent pour générer un espace de Hilbert H , au sens où la fermeture de leur étendue (c'est-à-dire , combinaisons linéaires finies et limites de celles-ci) est l'espace entier. Un tel ensemble de fonctions est appelé une base de H , sa cardinalité est connue sous le nom de dimension d'espace de Hilbert . Non seulement le théorème présente des fonctions de base appropriées comme suffisantes à des fins d'approximation, mais aussi avec le processus de Gram – Schmidt , il permet de construire une base de vecteurs orthogonaux . Ces bases orthogonales sont la généralisation de l'espace de Hilbert des axes de coordonnées dans l'espace euclidien de dimension finie .
Les solutions de diverses équations différentielles peuvent être interprétées en termes d'espaces de Hilbert. Par exemple, de nombreux domaines de la physique et de l'ingénierie conduisent à de telles équations et fréquemment des solutions aux propriétés physiques particulières sont utilisées comme fonctions de base, souvent orthogonales. À titre d'exemple de la physique, l' équation de Schrödinger dépendante du temps en mécanique quantique décrit le changement des propriétés physiques dans le temps au moyen d'une équation différentielle partielle , dont les solutions sont appelées fonctions d'onde . Les valeurs définies pour les propriétés physiques telles que l'énergie ou la quantité de mouvement correspondent aux valeurs propres d'un certain opérateur différentiel (linéaire) et les fonctions d'onde associées sont appelées états propres . Le théorème spectral décompose un opérateur compact linéaire agissant sur les fonctions en fonction de ces fonctions propres et de leurs valeurs propres.
Algèbres sur les champs

Les espaces vectoriels généraux ne possèdent pas de multiplication entre les vecteurs. Un espace vectoriel équipé d'un opérateur bilinéaire supplémentaire définissant la multiplication de deux vecteurs est une algèbre sur un champ . De nombreuses algèbres proviennent de fonctions sur certains objets géométriques: puisque les fonctions avec des valeurs dans un champ donné peuvent être multipliées par point, ces entités forment des algèbres. Le théorème de Stone-Weierstrass, par exemple, repose sur des algèbres de Banach qui sont à la fois des espaces et des algèbres de Banach.
L'algèbre commutative fait un grand usage des anneaux de polynômes dans une ou plusieurs variables, présentées ci-dessus . Leur multiplication est à la fois commutative et associative . Ces anneaux et leurs quotients forment la base de la géométrie algébrique , car ce sont des anneaux de fonctions d'objets géométriques algébriques .
Un autre exemple crucial sont les algèbres de Lie , qui ne sont ni commutatives ni associatives, mais le défaut de l'être est limité par les contraintes ( [ x , y ] désigne le produit de x et y ):
- [ x , y ] = - [ y , x ] ( anticommutativité ), et
- [ x , [ y , z ]] + [ y , [ z , x ]] + [ z , [ x , y ]] = 0 ( identité Jacobi ).
Les exemples incluent l'espace vectoriel de n -by- n matrices, avec [ x , y ] = xy - yx , le commutateur de deux matrices, et R 3 , doté du produit croisé .
L' algèbre tensorielle T ( V ) est une manière formelle d'ajouter des produits à n'importe quel espace vectoriel V pour obtenir une algèbre. En tant qu'espace vectoriel, il est couvert par des symboles, appelés tenseurs simples
- v 1 ⊗ v 2 ⊗ ⋯ ⊗ v n , où le degré n varie.
La multiplication est donnée en concaténant de tels symboles, en imposant la loi de distribution sous addition, et en exigeant que la multiplication scalaire commute avec le produit tensoriel ⊗, à peu près de la même manière qu'avec le produit tensoriel de deux espaces vectoriels introduit ci-dessus . En général, il n'y a pas de relations entre v 1 ⊗ v 2 et v 2 ⊗ v 1 . Forcer deux de ces éléments à être égaux conduit à l' algèbre symétrique , alors que forcer v 1 ⊗ v 2 = - v 2 ⊗ v 1 donne l' algèbre extérieure .
Lorsqu'un champ, F est explicitement indiqué, un terme couramment utilisé est F -algebra.
Applications
Les espaces vectoriels ont de nombreuses applications car ils se produisent fréquemment dans des circonstances courantes, à savoir partout où des fonctions avec des valeurs dans certains domaines sont impliquées. Ils fournissent un cadre pour traiter des problèmes analytiques et géométriques, ou sont utilisés dans la transformée de Fourier. Cette liste n'est pas exhaustive: de nombreuses autres applications existent, par exemple en optimisation . Le théorème minimax de la théorie des jeux affirmant l'existence d'un gain unique lorsque tous les joueurs jouent de manière optimale peut être formulé et prouvé en utilisant des méthodes d'espaces vectoriels. La théorie de la représentation transfère avec succès la bonne compréhension de l'algèbre linéaire et des espaces vectoriels à d'autres domaines mathématiques tels que la théorie des groupes .
Distributions
Une distribution (ou fonction généralisée ) est une application linéaire attribuant un nombre à chaque fonction "test" , typiquement une fonction lisse avec support compact , de manière continue: dans la terminologie ci - dessus, l'espace des distributions est le dual (continu) du espace des fonctions de test. Ce dernier espace est doté d'une topologie qui prend en compte non seulement f lui-même, mais aussi toutes ses dérivées supérieures. Un exemple standard est le résultat de l'intégration d'une fonction de test f sur un domaine Ω:
Lorsque Ω = { p }, l'ensemble constitué d'un seul point, cela se réduit à la distribution de Dirac , notée δ, qui associe à une fonction de test f sa valeur au p : δ ( f ) = f ( p ) . Les distributions sont un instrument puissant pour résoudre les équations différentielles. Puisque toutes les notions analytiques standard telles que les dérivées sont linéaires, elles s'étendent naturellement à l'espace des distributions. Par conséquent, l'équation en question peut être transférée dans un espace de distribution, qui est plus grand que l'espace de fonction sous-jacent, de sorte que des méthodes plus flexibles soient disponibles pour résoudre l'équation. Par exemple, les fonctions et les solutions fondamentales de Green sont généralement des distributions plutôt que des fonctions appropriées, et peuvent ensuite être utilisées pour trouver des solutions de l'équation avec des conditions aux limites prescrites. La solution trouvée peut alors être prouvée dans certains cas comme étant en fait une fonction vraie, et une solution à l'équation d'origine (par exemple, en utilisant le théorème de Lax – Milgram , une conséquence du théorème de représentation de Riesz ).
Analyse de Fourier
La résolution d'une fonction périodique en une somme de fonctions trigonométriques forme une série de Fourier , une technique très utilisée en physique et en ingénierie. L'espace vectoriel sous-jacent est généralement l' espace de Hilbert L 2 (0, 2π), pour lequel les fonctions sin mx et cos mx ( m un entier) forment une base orthogonale. L' expansion de Fourier d'une fonction L 2 f est
Les coefficients a m et b m sont appelés coefficients de Fourier de f , et sont calculés par les formules
- ,
En termes physiques, la fonction est représentée comme une superposition d' ondes sinusoïdales et les coefficients donnent des informations sur le spectre de fréquences de la fonction . Une forme de nombre complexe de séries de Fourier est également couramment utilisée. Les formules concrètes ci-dessus sont les conséquences d'une dualité mathématique plus générale appelée dualité de Pontryagin . Appliqué au groupe R , il donne la transformée de Fourier classique; une application en physique sont les réseaux réciproques , où le groupe sous-jacent est un espace vectoriel réel de dimension finie doté de la donnée supplémentaire d'un réseau codant les positions des atomes dans les cristaux .
Les séries de Fourier sont utilisées pour résoudre des problèmes de valeurs aux limites dans des équations aux dérivées partielles . En 1822, Fourier a utilisé cette technique pour la première fois pour résoudre l' équation de la chaleur . Une version discrète de la série de Fourier peut être utilisée dans des applications d' échantillonnage où la valeur de la fonction n'est connue qu'en un nombre fini de points également espacés. Dans ce cas, la série de Fourier est finie et sa valeur est égale aux valeurs échantillonnées en tous points. L'ensemble de coefficients est connu sous le nom de transformée de Fourier discrète (DFT) de la séquence d'échantillons donnée. Le DFT est l'un des outils clés du traitement numérique du signal , un domaine dont les applications incluent le radar , le codage de la parole , la compression d'image . Le format d' image JPEG est une application de la transformation cosinus discrète étroitement liée .
La transformée de Fourier rapide est un algorithme permettant de calculer rapidement la transformée de Fourier discrète. Il est utilisé non seulement pour calculer les coefficients de Fourier mais, en utilisant le théorème de convolution , aussi pour calculer la convolution de deux suites finies. Ils sont à leur tour appliqués dans des filtres numériques et comme algorithme de multiplication rapide pour les polynômes et les grands entiers ( algorithme de Schönhage – Strassen ).
Géométrie différentielle

Le plan tangent à une surface en un point est naturellement un espace vectoriel dont l'origine est identifiée avec le point de contact. Le plan tangent est la meilleure approximation linéaire , ou linéarisation , d'une surface en un point. Même dans un espace euclidien en trois dimensions, il n'y a généralement pas de moyen naturel de prescrire une base du plan tangent, et il est donc conçu comme un espace vectoriel abstrait plutôt qu'un espace de coordonnées réel. L' espace tangent est la généralisation aux variétés différentiables de dimension supérieure .
Les variétés riemanniennes sont des variétés dont les espaces tangents sont dotés d'un produit interne approprié . Dérivé de celui-ci, le tenseur de courbure de Riemann encode toutes les courbures d'une variété en un seul objet, qui trouve des applications en relativité générale , par exemple, où le tenseur de courbure d'Einstein décrit la matière et le contenu énergétique de l' espace-temps . L'espace tangent d'un groupe de Lie peut recevoir naturellement la structure d'une algèbre de Lie et peut être utilisé pour classer des groupes de Lie compacts .
Généralisations
Bundles de vecteur
Un fibré est une famille d'espaces vectoriels paramétrées en continu par un espace topologique X . Plus précisément, un fibré vectoriel sur X est un espace topologique E équipé d'une carte continue
- π: E → X
tel que pour tout x dans X , la fibre π −1 ( x ) est un espace vectoriel. Le cas dim V = 1 est appelé un faisceau de lignes . Pour tout espace vectoriel V , la projection X × V → X fait du produit X × V un fibré vectoriel "trivial" . Les faisceaux vectoriels sur X doivent être localement un produit de X et d'un espace vectoriel (fixe) V : pour tout x dans X , il existe un voisinage U de x tel que la restriction de π à π −1 ( U ) est isomorphe au faisceau trivial U × V → U . Malgré leur caractère localement trivial, les faisceaux vectoriels peuvent (selon la forme de l'espace sous-jacent X ) être «tordus» dans le grand (c'est-à-dire que le faisceau n'a pas besoin d'être (globalement isomorphe à) le paquet trivial X × V ). Par exemple, la bande de Möbius peut être vue comme un faisceau de lignes sur le cercle S 1 (en identifiant les intervalles ouverts avec la ligne réelle ). Il est cependant différent du cylindre S 1 × R , car ce dernier est orientable alors que le premier ne l'est pas.
Les propriétés de certains ensembles de vecteurs fournissent des informations sur l'espace topologique sous-jacent. Par exemple, le fibré tangent consiste en la collection d' espaces tangents paramétrés par les points d'une variété différentiable. Le fibré tangent du cercle S 1 est globalement isomorphe à S 1 × R , car il existe un champ de vecteurs global non nul sur S 1 . En revanche, par le théorème de la boule velue , il n'y a pas de champ vectoriel (tangent) sur la sphère 2 S 2 qui est partout non nul. La théorie K étudie les classes d'isomorphisme de tous les faisceaux vectoriels sur un certain espace topologique. En plus de l' approfondissement de vision topologique et géométrique, cela a des conséquences purement algébriques, telles que la classification des réel de dimension finie division algèbres : R , C , la quaternions H et le octonions O .
Le faisceau cotangent d'une variété différentiable se compose, en chaque point de la variété, du dual de l'espace tangent, l' espace cotangent . Les sections de cet ensemble sont appelées formes uniques différentielles .
Modules
Les modules sont aux anneaux ce que les espaces vectoriels sont aux champs: les mêmes axiomes, appliqués à un anneau R au lieu d'un champ F , donnent des modules. La théorie des modules, comparée à celle des espaces vectoriels, est compliquée par la présence d'éléments d'anneau qui n'ont pas d' inverses multiplicatifs . Par exemple, les modules n'ont pas besoin d'avoir des bases, comme le montre le module Z (c'est-à-dire le groupe abélien ) Z / 2 Z ; les modules qui le font (y compris tous les espaces vectoriels) sont appelés modules libres . Néanmoins, un espace vectoriel peut être défini de manière compacte comme un module sur un anneau qui est un champ , les éléments étant appelés vecteurs. Certains auteurs utilisent le terme espace vectoriel pour désigner les modules sur un anneau de division . L'interprétation algébro-géométrique des anneaux commutatifs via leur spectre permet le développement de concepts tels que les modules localement libres , le pendant algébrique des faisceaux vectoriels.
Espaces affines et projectifs
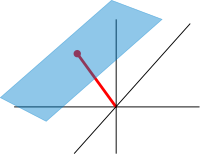
En gros, les espaces affines sont des espaces vectoriels dont les origines ne sont pas spécifiées. Plus précisément, un espace affine est un ensemble avec une action d' espace vectoriel transitif libre . En particulier, un espace vectoriel est un espace affine sur lui-même, par la carte
- V × V → V , ( v , a ) ↦ a + v .
Si W est un espace vectoriel, alors un sous-espace affine est un sous-ensemble de W obtenu en traduisant un sous-espace linéaire V par un vecteur fixe x ∈ W ; cet espace est désigné par x + V (elle est une classe d' équivalence de V dans W ) et se compose de tous les vecteurs de la forme x + v pour v ∈ V . Un exemple important est l'espace des solutions d'un système d'équations linéaires non homogènes
- A x = b
généralisant le cas homogène b = 0 ci-dessus . L'espace des solutions est le sous-espace affine x + V où x est une solution particulière de l'équation, et V est l'espace des solutions de l'équation homogène (l' espace nul de A ).
L'ensemble des sous-espaces unidimensionnels d'un espace vectoriel fixe de dimension finie V est appelé espace projectif ; il peut être utilisé pour formaliser l'idée de droites parallèles se croisant à l'infini. Les grassmanniens et les variétés de drapeaux généralisent cela en paramétrant respectivement des sous-espaces linéaires de dimension fixe k et des drapeaux de sous-espaces.
Voir également
- Vector (mathématiques et physique) , pour une liste de différents types de vecteurs
|
|
|
|
Remarques
Citations
Les références
Algèbre
- Artin, Michael (1991), Algèbre , Prentice Hall , ISBN 978-0-89871-510-1
- Blass, Andreas (1984), "L'existence de bases implique l'axiome du choix", Théorie des ensembles axiomatiques (Boulder, Colorado, 1983) , Contemporary Mathematics, 31 , Providence, RI: American Mathematical Society , pp. 31–33, MR 0763890
- Brown, William A. (1991), Matrices et espaces vectoriels , New York: M. Dekker, ISBN 978-0-8247-8419-5
- Lang, Serge (1987), Algèbre linéaire , Berlin, New York: Springer-Verlag , ISBN 978-0-387-96412-6
- Lang, Serge (2002), Algebra , Graduate Texts in Mathematics , 211 (troisième éd. Révisé), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
- Mac Lane, Saunders (1999), Algebra (3e éd.), Pp. 193-222, ISBN 978-0-8218-1646-2
- Meyer, Carl D. (2000), Analyse matricielle et algèbre linéaire appliquée , SIAM , ISBN 978-0-89871-454-8
- Roman, Steven (2005), Advanced Linear Algebra , Graduate Texts in Mathematics, 135 (2e éd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-24766-3
- Spindler, Karlheinz (1993), Algèbre abstraite avec applications: Volume 1: Espaces vectoriels et groupes , CRC, ISBN 978-0-8247-9144-5
- van der Waerden, Bartel Leendert (1993), Algebra (en allemand) (9e éd.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-56799-8
Une analyse
- Bourbaki, Nicolas (1987), Espaces vectoriels topologiques , Éléments de mathématiques, Berlin, New York: Springer-Verlag , ISBN 978-3-540-13627-9
- Bourbaki, Nicolas (2004), Intégration I , Berlin, New York: Springer-Verlag , ISBN 978-3-540-41129-1
- Braun, Martin (1993), Equations différentielles et leurs applications: une introduction aux mathématiques appliquées , Berlin, New York: Springer-Verlag , ISBN 978-0-387-97894-9
- BSE-3 (2001) [1994], "Plan tangent" , Encyclopédie de mathématiques , EMS Press
- Choquet, Gustave (1966), Topologie , Boston, MA: Academic Press
- Dennery, Philippe; Krzywicki, Andre (1996), Mathématiques pour les physiciens , Courier Dover Publications, ISBN 978-0-486-69193-0
- Dudley, Richard M. (1989), Analyse réelle et probabilité , The Wadsworth & Brooks / Cole Mathematics Series, Pacific Grove, Californie: Wadsworth & Brooks / Cole Advanced Books & Software, ISBN 978-0-534-10050-6
- Dunham, William (2005), The Calculus Gallery , Princeton University Press , ISBN 978-0-691-09565-3
- Evans, Lawrence C. (1998), Equations aux dérivées partielles , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0772-9
- Folland, Gerald B. (1992), Analyse de Fourier et ses applications , Brooks-Cole, ISBN 978-0-534-17094-3
- Gasquet, Claude; Witomski, Patrick (1999), Analyse de Fourier et applications: filtrage, calcul numérique, ondelettes , textes en mathématiques appliquées, New York: Springer-Verlag, ISBN 978-0-387-98485-8
- Ifeachor, Emmanuel C .; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2e éd.), Harlow, Essex, Angleterre: Prentice-Hall (publié en 2002), ISBN 978-0-201-59619-9
- Krantz, Steven G. (1999), A Panorama of Harmonic Analysis , Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
- Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6e éd.), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
- Kreyszig, Erwin (1989), Introduction à l'analyse fonctionnelle avec applications , Wiley Classics Library, New York: John Wiley & Sons , ISBN 978-0-471-50459-7, MR 0992618
- Lang, Serge (1983), Analyse réelle , Addison-Wesley , ISBN 978-0-201-14179-5
- Lang, Serge (1993), Analyse réelle et fonctionnelle , Berlin, New York: Springer-Verlag , ISBN 978-0-387-94001-4
- Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis , Toronto-New York-London: D. Van Nostrand Company, Inc., pp. X + 190, hdl : 2027 / uc1.b4250788
- Narici, Lawrence ; Beckenstein, Edward (2011). Espaces vectoriels topologiques . Mathématiques pures et appliquées (deuxième éd.). Boca Raton, Floride: CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- Schaefer, Helmut H .; Wolff, Manfred P. (1999). Espaces vectoriels topologiques . GTM . 8 (deuxième éd.). New York, NY: Springer New York Mentions légales Springer. ISBN 978-1-4612-7155-0. OCLC 840278135 .CS1 maint: ref = harv ( lien )
- Trèves, François (6 août 2006) [1967]. Espaces vectoriels topologiques, distributions et noyaux . Mineola, NY: Publications de Douvres. ISBN 978-0-486-45352-1. OCLC 853623322 .CS1 maint: ref = harv ( lien ) CS1 maint: date et année ( lien )
Références historiques
- Banach, Stefan (1922), «Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales)» (PDF) , Fundamenta Mathematicae (en français), 3 : 133– 181, doi : 10.4064 / fm-3-1-133-181 , ISSN 0016-2736
- Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considérations sur certains aspects de la géométrie élémentaire) (en allemand)
- Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (en français), Paris: Hermann
- Dorier, Jean-Luc (1995), "Un aperçu général de la genèse de la théorie de l'espace vectoriel" , Historia Mathematica , 22 (3): 227-261, doi : 10.1006 / hmat.1995.1024 , MR 1347828
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (en français), Chez Firmin Didot, père et fils
- Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (en allemand), O. Wigand, réimpression: Hermann Grassmann. Traduit par Lloyd C. Kannenberg. (2000), Kannenberg, LC (éd.), Extension Theory , Providence, RI: American Mathematical Society , ISBN 978-0-8218-2031-5
- Hamilton, William Rowan (1853), Conférences sur les quaternions , Royal Irish Academy
- Möbius, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Calcul barycentrique: un nouvel utilitaire pour un traitement analytique de la géométrie) (en allemand), archivé de l'original le 2006-11-23
- Moore, Gregory H. (1995), «L'axiomatisation de l'algèbre linéaire: 1875–1940», Historia Mathematica , 22 (3): 262–303, doi : 10.1006 / hmat.1995.1025
- Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (en italien), Turin
- Peano, G. (1901) Formulario mathematico : axiomes vct via Internet Archive
Autres références
- Ashcroft, Neil ; Mermin, N.David (1976), Solid State Physics , Toronto: Thomson Learning, ISBN 978-0-03-083993-1
- Atiyah, Michael Francis (1989), K-théorie , Advanced Book Classics (2e éd.), Addison-Wesley , ISBN 978-0-201-09394-0, MR 1043170
- Bourbaki, Nicolas (1998), Éléments de mathématiques: Algèbre I Chapitres 1-3 , Berlin, New York: Springer-Verlag , ISBN 978-3-540-64243-5
- Bourbaki, Nicolas (1989), Topologie générale. Chapitres 1-4 , Berlin, New York: Springer-Verlag , ISBN 978-3-540-64241-1
- Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2e éd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-96532-1
- Eisenberg, Murray; Guy, Robert (1979), "Une preuve du théorème de la boule velue", The American Mathematical Monthly , 86 (7): 572–574, doi : 10.2307 / 2320587 , JSTOR 2320587
- Eisenbud, David (1995), Algèbre commutative , Textes de diplômés en mathématiques, 150 , Berlin, New York: Springer-Verlag , ISBN 978-0-387-94269-8, MR 1322960
- Goldrei, Derek (1996), Classic Set Theory: A Guided Independent Study (1ère éd.), Londres: Chapman and Hall , ISBN 978-0-412-60610-6
- Griffiths, David J. (1995), Introduction à la mécanique quantique , Upper Saddle River, NJ: Prentice Hall , ISBN 978-0-13-124405-4
- Halmos, Paul R. (1974), Espaces vectoriels de dimension finie , Berlin, New York: Springer-Verlag , ISBN 978-0-387-90093-3
- Halpern, James D. (juin 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society , 17 (3): 670–673, doi : 10.2307 / 2035388 , JSTOR 2035388
- Hughes-Hallett, Deborah; McCallum, William G .; Gleason, Andrew M. (2013), Calculus: Single and Multivariable (6 éd.), John Wiley & Sons , ISBN 978-0470-88861-2
- Husemoller, Dale (1994), Fiber Bundles (3e éd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-94087-8
- Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4e éd.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-25907-7
- Kreyszig, Erwin (1991), Géométrie différentielle , New York: Dover Publications , pp. Xiv + 352, ISBN 978-0-486-66721-8
- Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8e éd.), New York: John Wiley & Sons , ISBN 978-0-471-15496-9
- Luenberger, David (1997), Optimisation par les méthodes de l'espace vectoriel , New York: John Wiley & Sons , ISBN 978-0-471-18117-0
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2e éd.), Berlin, New York: Springer-Verlag , ISBN 978-0-387-98403-2
- Misner, Charles W .; Thorne, Kip ; Wheeler, John Archibald (1973), Gravitation , WH Freeman, ISBN 978-0-7167-0344-0
- Naber, Gregory L. (2003), La géométrie de l'espace - temps de Minkowski , New York: Dover Publications , ISBN 978-0-486-43235-9, MR 2044239
- Schönhage, A .; Strassen, Volker (1971), «Schnelle Multiplikation großer Zahlen (Multiplication rapide des grands nombres)», Computing (en allemand), 7 (3–4): 281–292, doi : 10.1007 / bf02242355 , ISSN 0010-485X
- Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two) , Houston, TX: Publish or Perish
- Stewart, Ian (1975), Galois Theory , Chapman and Hall Mathematics Series, Londres: Chapman et Hall , ISBN 978-0-412-10800-6
- Varadarajan, VS (1974), Groupes de Lie, Algèbres de Lie et leurs représentations , Prentice Hall , ISBN 978-0-13-535732-3
- Wallace, GK (février 1992), «The JPEG Still Picture Compression Standard» (PDF) , IEEE Transactions on Consumer Electronics , 38 (1): xviii – xxxiv, CiteSeerX 10.1.1.318.4292 , doi : 10.1109 / 30.125072 , ISSN 0098 -3063 , archivé de l'original (PDF) le 13/01/2007 , récupéré 25/10/2017
- Weibel, Charles A. (1994). Une introduction à l'algèbre homologique . Études de Cambridge en mathématiques avancées. 38 . La presse de l'Universite de Cambridge. ISBN 978-0-521-55987-4. MR 1269324 . OCLC 36131259 .
Liens externes
- "Espace vectoriel" , Encyclopédie des mathématiques , EMS Press , 2001 [1994]















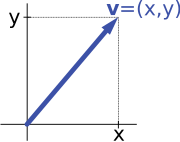


















































![{\ frac {a_ {0}} {2}} + \ sum _ {m = 1} ^ {\ infty} \ left [a_ {m} \ cos \ left (mx \ right) + b_ {m} \ sin \ gauche (mx \ droite) \ droite].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b02fb26ebada4babaa1d88e20bb63e3b370c13b3)


